Los datos tienen forma
Una de las primeras preguntas que nos podemos hacer al sentarnos delante de un conjunto de datos (o dataset) gira en torno a cómo están distribuidos los valores de las variables que componen el dataset. La pregunta se podría formular así: ¿qué forma tienen nuestros datos?
Lo que estamos buscando es saber si los datos están distribuidos uniformemente en el rango de valores de la variable, o si se distribuyen de alguna forma alrededor de su valor medio, o cualquier otra distribución menos intuitiva.
También estamos buscando si hay concentración de ocurrencias de ciertos valores en algún sub-rango de la variable, o incluso si existen varios sub-rangos en los que se concentran mayor número de valores.
Para responder a estas preguntas, y otras mucho más técnicas, nos podemos apoyar en una de las visualizaciones de referencia en el campo de la ciencia de datos: el histograma.
El histograma
Un histograma es una visualización que sirve para representar, en los típicos ejes XY, los valores una variable dentro de un dataset. En el eje X se representan los valores que puede tomar la variable que queremos visualizar, agrupados en rangos o clases (en un momento detallaremos más este punto). En el eje Y se representa la frecuencia o total de observaciones (datapoints) que cada rango o clase tiene respecto del total de valores.
Para hacer más llevadera nuestra explicación y ponerle un poco de intuición al asunto, vayamos directamente a un ejemplo. Vamos a ayudarnos de un dataset que contiene datos de todas las películas y series del catálogo de Netflix, aunque nos vamos a centrar solamente en las películas (4265 en total) y en la variable que indica la duración de cada una de ellas. Este dataset se puede encontrar aquí.
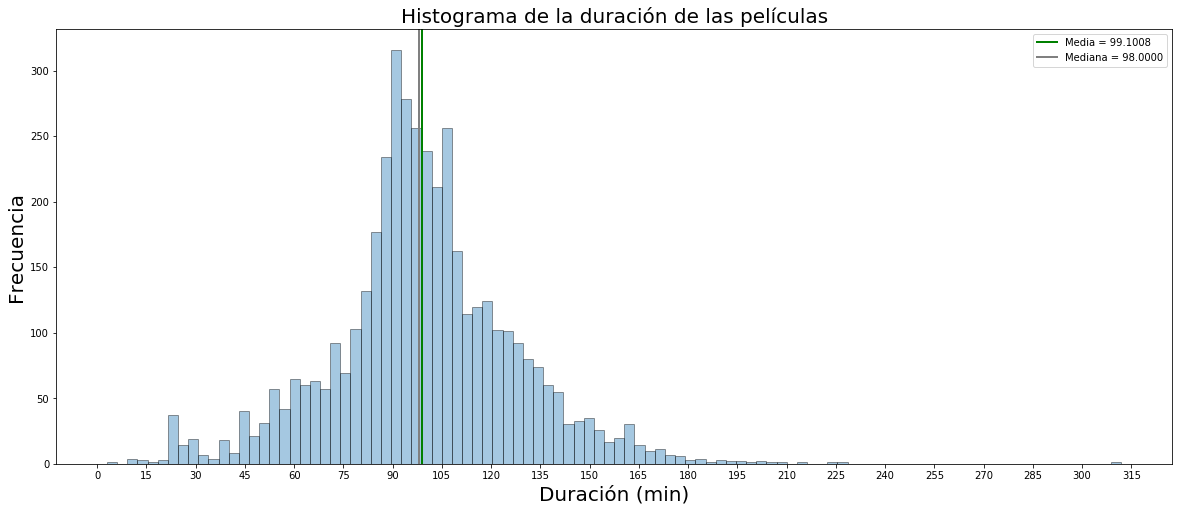
Antes de meternos en más tecnicismos, vayamos directamente a la visualización del histograma de la duración de las películas.
Aspectos técnicos del histograma
A partir de la visualización anterior, es mucho más fácil explicar los aspectos técnicos. En realidad no son muchos:
- Clases o categorías: son cada una de las «barritas» en las que está dividido el histograma. En inglés se denominan «bins«. El eje X es dividido en un número concreto de bins de longitud fija. Es decir, es «troceado» en intervalos contiguos que finalmente componen todo el rango.
- Total o Frecuencia: el eje Y representa la altura de cada bin, y dependerá del número de elementos (observaciones, datapoints) que haya en el rango del bin. Dependiendo de las fuentes donde consultéis, a esto se le llama total o frecuencia del bin.
- Simetría/asimetría: visualmente vamos a poder observar cómo se distribuyen las clases en términos de simetría, aunque hay dos métricas que nos van a ayudar a saber más de esta característica: la media y la mediana:
- La distribución se dice simétrica o está cerca de ser simétrica si media y mediana se encuentran cerca. Es importante remarcar que la interpretación de «cerca» va a depender de los propios datos. Por ejemplo, si estamos analizando la altura de la población adulta y el rango de altura va entre 80cm y 220cm, 140 y 185 son dos cifras que están lejos. Sin embargo, si estamos analizando la altura de los árboles y el rango va entre 100 y 2000cm, 140 y 185 son dos cifras que están cerca.
- La distribución se dice con sesgo a la derecha (skewed right) si la media es mayor que la mediana. Esto ocurre porque hay valores excesivamente grandes (a la derecha del rango) que «tiran» la media hacia la derecha, aunque la mediana permanezca inalterable.
- La distribución se dice con sesgo a la izquierda (skewed left) cuando la media es menor que la mediana. De forma análoga, hay valores excesivamente pequeños (a la izquierda del rango) que «tiran» de la media hacia la izquierda, aunque la mediana no se vea afectada.
Volvamos a Netflix
En el ejemplo de las películas de Netflix, la película con duración más corta es 3 minutos y la de duración más larga es 312 minutos. Hemos dividido el rango de la duración de las películas en 100 bins, de modo que aproximádamente cada bin abarca 3 minutos, así que estos serían aproximádamente los intervalos: [3-6), [6-9), [9,12), [12,15), …….[310,313)
La altura de cada barra va a depender del número de películas que haya dentro de cada intervalo. Por tanto, cuantas más películas haya en un intervalo determinado, más alta será la barra o bin.
Podemos observar que hay más de 300 películas que se encuentran en el entorno de los 90 minutos. Otra observación interesante es que la media de duración son 99 minutos (leyenda de arriba a la derecha), y que si ordenamos las 4265 películas por duración, la que se encuentra en el punto medio dura 98 minutos (mediana). Se encuentran «cerca», así que además de poder constatar visualmente que la distribución es equilibrada, los datos también nos lo confirman.
Si en vez de 100 clases/categorías/bins hubiéramos configurado 25, este sería el resultado:
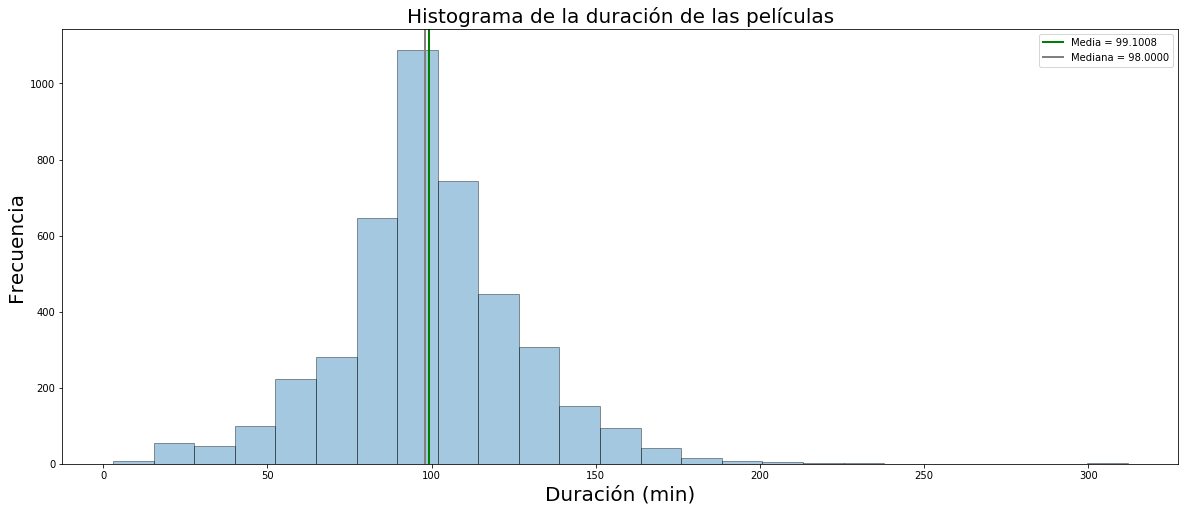
Al elegir 25 bins podemos ver de forma mucho más clara lo bien equilibrada que se encuentra la distribución de datos de duración de películas. En este caso vemos que el bin que está en el entorno a los 100 minutos contiene más de 1000 películas.
Se podría decir que es casi «normal» en el sentido que se asemeja bastante a la forma que tiene una distribución normal o gaussiana, con la típica forma de campana. Veamos.
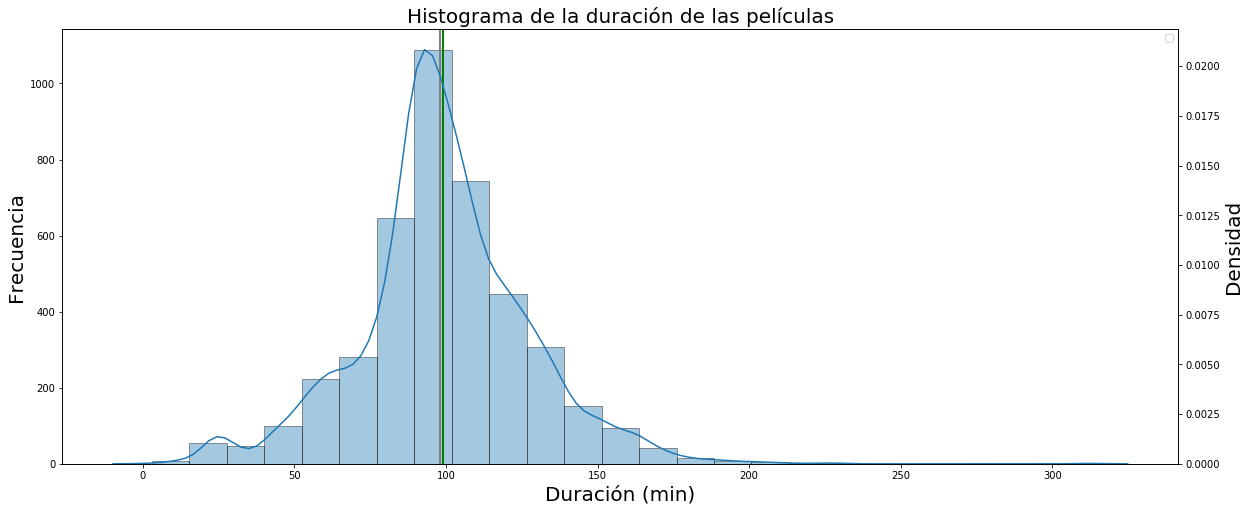
Si te interesa el código, aquí lo tienes
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import re # Function to plot an histogram def histogram_plot(example_arr, bins = 25, title = "", label = "", axis = None, show_density=False): axis.set_title(title, fontsize = 20) sns.distplot(example_arr, kde=False, bins=bins, ax=axis) if show_density: second_ax = axis.twinx() sns.distplot(example_arr, kde=True, hist=False, ax=second_ax) second_ax.set_ylabel("Densidad", fontsize = 20) axis.set_xlabel(label, fontsize = 20) axis.set_ylabel("Frecuencia", fontsize = 20) axis.xaxis.set_major_locator(plt.MaxNLocator(bins/3)) mean = np.mean(example_arr) median = np.median(example_arr) formatted_mean = "{:.4f}".format(mean) formatted_median = "{:.4f}".format(median) axis.axvline(mean, color='green', linewidth=2, linestyle='-', label = "Media = " + formatted_mean) axis.axvline(median, color='grey', linewidth=2, linestyle='-', label = "Mediana = " + formatted_median) plt.legend() def prepare_netflix_dataset(file_name): # Read the file netflix_catalogue_df = pd.read_csv(file_name) # Print unique values for the type of content print(netflix_catalogue_df['type'].unique()) # Keep only the movies netflix_catalogue_movies_df = netflix_catalogue_df[netflix_catalogue_df.type == 'Movie'] # Keep only the 'duration' variable netflix_catalogue_movies_duration = netflix_catalogue_movies_df.duration # The duration variable follows the pattern 'XX min'. Keep only the numeric value and convert it to integer netflix_catalogue_movies_duration = netflix_catalogue_movies_duration.str.extract('(\d+)', expand=False) netflix_catalogue_movies_duration = netflix_catalogue_movies_duration.astype(int) print("Rango de duración: [{}-{}]".format(netflix_catalogue_movies_duration.min(), netflix_catalogue_movies_duration.max())) # Return the processed variable return netflix_catalogue_movies_duration # Display preparation figure = plt.figure(figsize=(20, 8)) ax_histogram = figure.add_subplot(1, 1, 1) plt.rcParams["patch.force_edgecolor"] = True # File name file_name = "./Visualizaciones/Histograma/netflix_titles.csv" X = prepare_netflix_dataset(file_name) histogram_plot(X, bins = 25, title = "Histograma de la duración de las películas", label = "Duración (min)", axis = ax_histogram, show_density=True) |
Un ejemplo más
Es probable que os hayáis preguntado el significado de la imagen que encabeza el post. Es un homenaje a la distribución normal, a través de unas bonitas flores con forma de campana. Vamos a seguir haciendo uso de esta imagen para ver otro ejemplo práctico de los histogramas.
Los aficionados y profesionales de la fotografía recurren habitualmente a los histogramas para revisar el resultado de una imagen desde el punto de vista de brillo y desde el punto de vista de saturación de color (histograma RGB). Aquí nos vamos a detener un poco en el primer punto de vista, el histograma de brillo.
El histograma muestra la exposición de una imagen desde el punto de vista de la escala de grises. Por tanto, la «X» de nuestro histograma es el rango que abarca la escala de grises, siendo el negro el valor que está más «a la izquierda» y el blanco el valor que está más «a la derecha». La altura en el eje «Y» va a indicar cuántos pixeles de la imagen pertenecen a un sub-rango concreto de la escala de grises.
Una imagen se dice subexpuesta (tiene zonas sombrías u oscuras) cuando nos encontramos mucha concentración de valores (valores con Y alta) hacia la izquierda. Análogamente , una imagen se dice sobreexpuesta (tendrá zonas «quemadas») cuando hay mucha concentración de valores hacia la derecha, es decir, tiene muchos pixeles cerca del blanco. Una imagen que contenga todos los tonos de grises tendrá un histograma equilibrado a lo largo de todo el eje X.
En la imagen de cabecera del post, la escala de grises abarca el rango [0-255]. El 0 representa el negro y el 255 representa el blanco. Veamos el resultado.
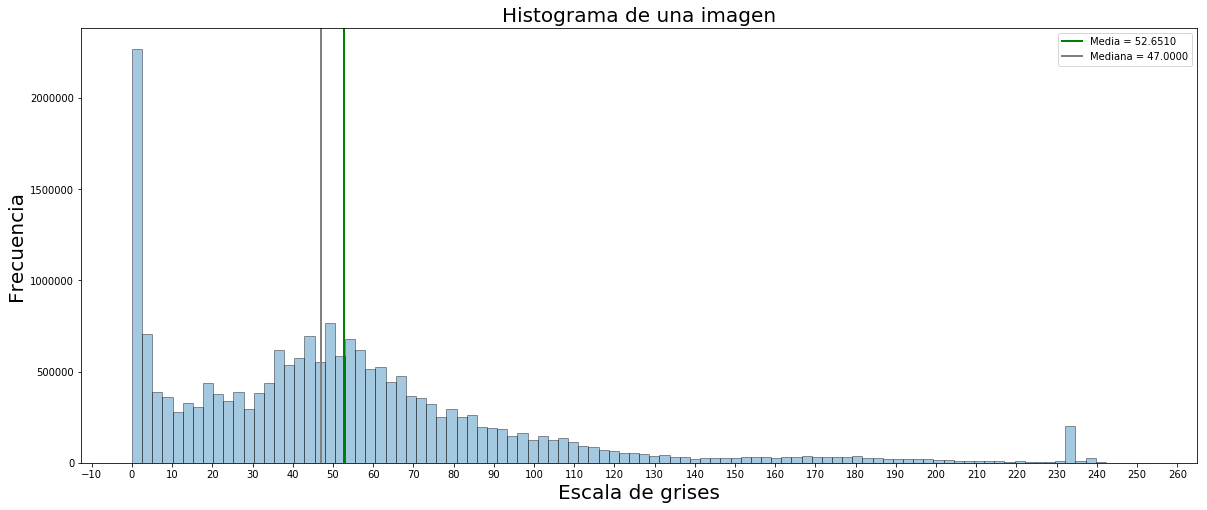
El histograma nos está confirmando lo que intuitivamente hemos visto: es una imagen donde predominan los tonos oscuros, ya que podemos observar la concentración de valores hacia la izquierda del histograma. De hecho, el color negro es el más predominante. Podemos ver también la larga «cola» de la distribución hacia la derecha, confirmándose el sesgo a la derecha, algo que también podemos saber porque la media es mayor que la mediana.
Si te interesa el código, aquí lo tienes
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import re import cv2 # Function to plot an histogram def histogram_plot(example_arr, bins = 25, title = "", label = "", axis = None, show_density=False): axis.set_title(title, fontsize = 20) sns.distplot(example_arr, kde=False, bins=bins, ax=axis) if show_density: second_ax = axis.twinx() sns.distplot(example_arr, kde=True, hist=False, ax=second_ax) second_ax.set_ylabel("Densidad", fontsize = 20) axis.set_xlabel(label, fontsize = 20) axis.set_ylabel("Frecuencia", fontsize = 20) axis.xaxis.set_major_locator(plt.MaxNLocator(bins/3)) mean = np.mean(example_arr) median = np.median(example_arr) formatted_mean = "{:.4f}".format(mean) formatted_median = "{:.4f}".format(median) axis.axvline(mean, color='green', linewidth=2, linestyle='-', label = "Media = " + formatted_mean) axis.axvline(median, color='grey', linewidth=2, linestyle='-', label = "Mediana = " + formatted_median) plt.legend() def prepare_image_dataset(file_name): # Read file and return it as matrix pixel image_matrix = cv2.imread(file_name) # calculate mean value from RGB channels and flatten to 1D array val_arr = image_matrix.mean(axis=2).flatten() # Return the processed variable return val_arr # Display preparation figure = plt.figure(figsize=(20, 8)) ax_histogram = figure.add_subplot(1, 1, 1) plt.rcParams["patch.force_edgecolor"] = True # File name file_name = "./Visualizaciones/Histograma/aaron-burden-gF_umQbT5tM-unsplash.jpg" X = prepare_image_dataset(file_name) histogram_plot(X, bins = 100, title = "Histograma de una imagen", label = "Escala de grises", axis = ax_histogram, show_density=False) |
Takeaway
Pocas visualizaciones pueden decir más de las propiedades de una variable con tan poco que configurar. Necesitamos, obviamente, la variable e indicar en cuántos bins, clases o categorías queremos dividir el rango de valores de la variable. A partir de ahí, se nos abre un mundo para interpretar la historia que nos cuenta el histograma.
Ver el primer bloque de código en Kaggle
Ver el segundo bloque de código en Kaggle

